Ссылки

Занятие 5-6

Различные системы счисления

 

 Ключевой вопрос занятия: «Всегда ли дважды два четыре?»  

          
Когда людям приходилось считать на пальцах очень большие совокупности предметов, к счёту привлекали больше участников. Один считал единицы, второй – десятки, а третий – сотни, то есть, десятки десятков. Такой счёт единицами, потом десятками, затем десятками десятков, а дальше десятками сотен и т.д. лёг в основу системы счисления, принятой почти у всех народов мира.

Сначала говорили так: пять пальцев третьего человека, восемь пальцев второго  и шесть пальцев первого. Но ведь это сколько времени надо произносить! Поэтому постепенно стали говорить короче. Вместо «палец второго человека» появилось слово «десять», вместо «палец  третьего человека» - «сто». Вот и получилось: пятьсот восемьдесят шесть.
Такую систему счисления называют позиционной десятичной системой. В ней за основание нумерации принято число 10 и соответственно этому имеется 10 различных знаков – цифр (0,1,2,3,4,5,6,7,8,9) для записи этих чисел. Значение цифры для чтения и записи числа зависит от её места, позиции в записи числа. Поэтому система счисления и называется позиционной. Так,  в числах 586, 352, 285 цифра «пять» стоит на разных местах и в зависимости от этого имеет различные значения: в первом числе она означает сотни, во втором -  десятки,  а в третьем – единицы.

Если за основание принять другое число, то получим другую систему счисления: восьмеричную, если за основание принять число 8 (соответственно будет всего 8 цифр – 0,1,2,3,4,5,6,7);  троичную, если за основание принять число 3 (соответственно будет всего 3 цифры – 0,1,2) и т.д.

В разное время употреблялись системы счисления, отличные от десятичной. Так, у вавилонян основанием системы счисления было число 60 (деление окружности на 360  градусов, 1 часа на 60 минут, 1 минуты на 60 секунд – это остатки вавилонской системы счисления). Двадцатеричная  система была распространена у древних римлян, у индийских племён Северной Америки, у туземных народов Центральной и Южной Америки. У народов Африки встречались пятеричная и двадцатеричная системы.

Некоторые недесятичные системы счисления используются и теперь. Так, широкое применение в электронных машинах, компьютерах, получила двоичная система счисления. Числа, записанные в этой системе, удобно вводить в компьютер и производить над ними действия для решения различных довольно сложных задач.

	Тест «Проверь себя!»
	1.  Система счисления – это: А) совокупность единиц измерения     Б) совокупность правил чтения и записи чисел       В) совокупность цифр 2. Практически все народы  мира пользуются системой счисления:
	А) пятеричной       Б) восьмеричной      В) десятичной
	3.  В пятеричной системе счисления используют цифры: А) 0,1,2,3,4,5 Б) 0,1,2,3,4, В) 0,1,2,3,4,5,6,7,8,9
	4. В каждой системе счисления наибольшая цифра: А) равна основанию системы Б) на единицу меньше основания   В) на единицу больше основания
	5. Широкое применение в электронных машинах получила А) двоичная система счисления Б) пятеричная система счисления В) десятичная система счисления

 

Трудно ли изображать числа в других системах? Нисколько. Для того, чтобы показать, в какой системе счисления записано число, справа внизу записывают основание системы счисления. Например, 10011₂; 243₅; 1357₈. Ты уже знаешь, что числа в десятичной системе записываются без указания основания: 235.
Основой перевода чисел из любой системы в десятичную является разложение их по разрядам (запись их в виде многочлена, расположенного по степеням основания системы).
Так, в десятичной системе счисления 235=200+30+5=2•10² +3•10 +5
Алгоритм перевода числа в десятичную систему счисления
1 способ
1. Разложить число по разрядам.
2. Найти  значение выражения, которое и будет являться представлением числа в десятичной системе.
Так, чтобы перевести 235₈ в десятичную систему счисления, разложим его по разрядам: 235₈=2•8² +3•8 +5.  Найдём значение этого выражения, оно равно 157. Значит,  235₈=157
2 способ
1. Единицы высшего разряда умножить на основание системы счисления.
2. К полученному результату прибавить единицы следующего разряда.
3. Полученную сумму умножить на основание системы.
4.  К полученному произведению прибавить единицы следующего разряда и умножить на основание системы и т.д.
5. К полученному произведению прибавить единицы первого разряда.
Проверим на числе 235₈.

x	2
	8
+	16
	3
x	19
	8
+	152
	5
	157

Значит, 235₈ =  157
1. Задание (3 балла)  Числа 1101₂; 222₃; 123₄  вырази в десятичной системе счисления. Проверь себя, выполнив упражнение разными способами.
2. Задание (5 баллов)  Проверь примеры
21420₅ = 1485
241₇ =126
120₃=1111₂
Внимание!  Чем отличается последний пример от первых двух?
Сделай важный вывод: как перевести число из одной системы счисления (недесятичной) в другую, отличную от десятичной системы.
Всякое число десятичной системы можно записать в системе с любым основанием. Например, надо число 119 изобразить в пятеричной системе. Делим 119 на 5, чтобы узнать, сколько в нём единиц первого разряда:
119: 5=23, остаток 4.
Значит, число простых единиц будет 4. Далее, 23 пятёрки не могут стоять все во втором разряде, так как высшая цифра в пятерично системе – 4, и больше 4 единиц ни в одном разряде быть не должно. Делим поэтому 23 на 5:
23:5 =4, остаток 3
Это показывает, что во втором разряде («пятёрок») будет цифра 3, а в третьем («пятёрок в квадрате») цифра – четыре. Итак, 119=4•5²+3•5+4 =4345
Для удобства такие преобразования выполняют столбиком:

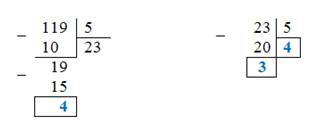
Внимание! Подумай, какие важные моменты (правила) надо знать, чтобы правильно записать число десятичной системы в системе с любым основанием.

3. Задание (3балла)  Представить числа:
47 в троичной системе счисления
200 в семеричной системе  счисления
163 в двенадцатеричной системе счисления
4. Задание (3балла)  Записать числа в двоичной системе: 253, 478, 2372  
5.Задание (4балла)  Записать числа в двоичной системе: 12013; 30124; 4238
6. Задание (5баллов)  Найдите основание системы счисления 43х=27, 25х=17, 123х=27

Задача на сообразительность (20 баллов)
В бумагах одного чудака – математика найдена была
его автобиография.    Она начиналась следующими
удивительными строками:

«Я окончил курс университета 44 лет отроду.  Спустя год, 100-летним молодым человеком, я женился на 34-летней девушке. Незначительная разница в возрасте – всего 11 лет – способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и маленькая семья из 10 детей. Жалования я получал в месяц всего 200 рублей, из которых 1/10 приходилось отдавать сестре, так что мы с детьми жили на 130 рублей в месяц» и т.д.
Чем объяснить странные противоречия этой автобиографии?
Найди фразу из отрывка, которая раскрывает секрет письма.
Перепишите эти строки, восстановив истинный смысл записи.

Творческая мастерская «Придумай сам»
1. Придумай задания разного характера на тему «Системы счисления».
2. Разработай алгоритм сложения и вычитания чисел недесятичной системы счисления.
Внимание!Не забудь разместить их на форуме «Математическая копилка» для обсуждения.

Пришло время ответить на ключевой вопрос занятия:
       «Всегда ли дважды два четыре?» Докажите.

Заполни Лист Мои достижения и выбери модель, которая соответствует самооценке твоего уровня знаний и умений по теме «Различные системы счисления».

 

На этих занятиях ты научился работать с различными системами счисления. Если у тебя возникли вопросы, задай их на форуме «Нужна консультация».

Теперь ты можешь показать  родителям, друзьям, как число можно представить в другой системе счисления. Не забудь, что здесь очень важно правильно определить по основанию системы наибольшую цифру и место (позицию) каждой цифры, какой разряд она означает. Знания разрядов тебе потребуется и на следующем занятии, так как мы будем знакомиться с числами - великанами и с числами - лилипутами. Постарайся привести примеры таких чисел.