Занятие 13-14
Математическая олимпиада
Сегодня ты начинаешь работать
с заключительным разделом курса «Загадки в мире чисел или занимательная арифметика», который называется «Мои достижения»
На этих занятиях тебе предстоит продемонстрировать свои успехи, показать знания и умения – всё то, чему ты научился в рамках курса.
Прими наши поздравления в связи с твоим участием в математической олимпиаде. В течение двух занятий ты со своими сверстниками должен выполнить две олимпиадные работы. Одна работа состоит из заданий с открытым ответом, другая – из заданий с вариантами ответов.
Каждое задание оценено от 3-х до 5 -ти баллов, поэтому ты сможешь сам подсчитать общее количество заработанных очков (при условии, что задание выполнено правильно). Постарайся набрать как можно больше баллов, по итогам олимпиады будут определены победители.
Олимпиадная работа № 1
Задачи, оцениваемые в 3 балла
Задание 1. Вместо звёздочек поставь нужные цифры, чтобы число делилось на 6 без остатка: *357**
Задание 2. Написаны подряд цифры 1, 2, 3, 4, 5. Не меняя порядка цифр, вставить между ними знаки арифметических действий, чтобы получилось число 100.
Задание 3. Сколько чисел по правилам римской нумерации можно записать с помощью цифр I; V; X?
Задачи, оцениваемые в 4 балла
Задание 4. Поезд длиной в 450 м проходит мост за 35 сек и проходит мимо дежурного по станции за 15 с. Найти длину моста и скорость поезда.
Задание 5. В четырёх пакетах лежат по одинаковому числу конфет. Если из каждого вынуть по 9 конфет, то во всех останется столько, сколько было в каждом. Сколько конфет было в каждом пакете?
Задание 6. Лёня, Женя и Миша имеют фамилии Орлов, Соколов, Ястребов. Какую фамилию имеет каждый мальчик, если Женя, Миша и Соколов члены математического кружка, а Миша и Ястребов занимаются музыкой?
Задачи, оцениваемые в 5 баллов
Задание 7. Существует ли система счисления, в которой одновременно:
а) 3 + 4 = 10 и 3 • 4 = 15?
б) 2 + 3 = 5 и 2 • 3 = 11?
Задание 8. Отцу 41 год, старшему сыну13 лет, дочери 10 лет, а младшему сыну 6 лет. Через сколько лет возраст отца окажется равным сумме лет его детей?
Задание 9. Если в фразе, представляющей зашифрованное сложение: «РЕШИ, ЕСЛИ СИЛЕН», каждую букву заменить соответствующей цифрой, то сумма чисел «РЕШИ» и «ЕСЛИ» окажется числом, выражаемым словом: «СИЛЕН». При этом известно, что наибольшая цифра в числе «СИЛЕН» равна 5. Найти слагаемые и сумму.
Олимпиадная работа № 2
Задачи, оцениваемые в 3 балла
Задание 1. Вася хочет написать слово КЕНГУРУ. Он начал писать в среду и пишет по одной букве в день. В какой день недели Вася напишет последнюю букву?
(А) понедельник (Б) вторник (В) среда
(Г) четверг (Д) пятница
Задание 2. Через три с половиной часа отправляется поезд, на котором Сёма поедет к бабушке. Боясь проспать, он проснулся полтора часа назад. За сколько часов до отправления поезда Сёма проснулся?
(А) за полтора часа (Б) за 2 часа (В) за 3 с половиной часа
(Г) за 4 часа (Д) за 5 часов
Задание 3. 2•0•11 + 20•11 - 201•1 = ?
(А) 0 (Б) 19 (В) 31 (Г) 421 (Д) 423
Задание 4. У Димы в кармане 5 монет, каждая либо 5 рублей, либо 10 рублей. Сколько денег всего может быть у него в кармане?
(А) 30 руб. (Б) 37 руб. (В) 45 руб. (Г) 57 руб. (Д) 75 руб.
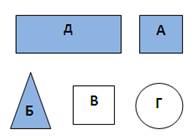
Задание 5.
Про одну из пяти карточек, нарисованных справа, Маша сказала: «Она не квадратная и не белая, она круглая или треугольная». Какая это карточка? (А) А (Б) Б (В) В (Г) Г (Д) Д
|
|
Задание 6. Электронные часы показывают часы и минуты. Сколько всего раз с 7 часов до 23 часов они покажут четыре одинаковых цифры?
(А) 1 (Б) 2 (В) 3 (Г) 5 (Д) 12
Задачи, оцениваемые в 4 балла
Задание 7. Квадратный лист бумаги разделили на две части одним прямым разрезом. Какая из фигур А-Г не могла при этом получиться?
(А) шестиугольник (Б) пятиугольник (В) прямоугольник
(Г) треугольник (Д) все фигуры А – Г могут получиться
Задание 8. В кувшине в пять раз больше воды, чем в чайнике, а в чайнике на 8 стаканов воды меньше, чем в кувшине. Сколько стаканов воды в кувшине и чайнике вместе?
(А) 12 (Б) 14 (В) 16 (Г) 18 (Д) 20
Задание 9.
Из трёх карточек, изображённых справа, можно составлять числа, например, 989 или 986. Сколько всего различных трёхзначных чисел можно составить из этих карточек? (А) 12 (Б) 9 (В) 8 (Г) 6 (Д) 4 |
|
Задание 10. В комнате 12 щенков, каждый из них шумный или кусачий. Кусачих щенков 8, а шумных – 9. Сколько среди них шумных и кусачих одновременно?
(А) 3 (Б) 4 (В)5 (Г) 6 (Д) 8
Задание 11. Никита терпеливо выписал все трёхзначные числа, цифры которых идут в убывающем порядке. Чему равна разность между самым большим и самым маленьким из этих чисел?
(А) 665 (Б) 777 (В) 800 (Г) 899 (Д) 966
Задачи, оцениваемые в 5 баллов
Задание 12. Саша вписал числа 1, 2, 3, 4, 5, 6, 7, 8 в кружочки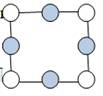
Оказалось, что сумма чисел, стоящих на каждой стороне
квадрата, равна 13. Чему равна сумма чисел в закрашенных
кружочках?
(А) 12 (Б) 13 (В) 14 (Г) 16 (Д) 20
Задание 13. В некотором месяце было 5 четвергов и 5 пятниц, но всего 4 субботы, 4 воскресенья и 4 понедельника. Тогда в следующем месяце будет
(А) 5 вторников (Б) 5 сред (В) 5 четвергов
(Г) 5 пятниц (Д) 5 суббот
Задание 14. В числовом ребусе буквами K, A, N, G, R, O 
обозначены разные цифры. Сколько различных значений
может принимать буква К?
(А) 1 (Б) 2 (В) 3 (Г) 4 (Д) 5
Задание 15. Стерев в числе 20311 цифру 3, получим число 2011. Сколько всего существует пятизначных чисел, из которых можно получить число 2011, удалив одну цифру?
(А) 45 (Б) 46 (В) 48 (Г) 49 (Д) 50
Вот и закончилась математическая олимпиада. На следующем занятии будут подведены итоги, названы победители.
Подумай, какие задания ты решил легко и быстро, на какие упражнения у тебя ушло много времени и сил, а с какими задачами так и не смог справиться. На следующем занятии попытаемся вместе решить твои проблемы.