Множества
Одно из основных понятий математики – множества.  Когда говорят о множестве, то объединяют в одну группы предметы или понятии по какому-либо признаку и рассматривают эту группу объектов как одно целое.
Основатель теории множеств, немецкий математик Георг Кантор (1845 -1918гг.) писал:  «Множество есть многое, мыслимое как единое целое».
Слово «множество» в обычном понимании всегда связывается с большим числом предметов. Например, мы говорим, что в лесу множество деревьев, но если перед домом два дерева, в повседневной речи не говорят, что перед домом «множество» деревьев.
Математическое понятие множества не связывается с большим числом предметов. В математике удобно рассматривать множества, содержащие три, два или один предмет, и даже множество, не содержащее ни одного предмета.
Например, множество   сооружений на Земле высотой более 500 метров состоит из одного элемента, а множество   сооружений,  высотой более 800 метров, не содержит ни одного элемента.
Об объектах, составляющих множество, говорят, что они принадлежат этому множеству или являются его элементами.
Элементами множества могут быть объекты различной природы (буквы, числа, фигуры,  люди, слова, точки, уравнения и т.д.)
Множества, элементами которых являются числа, называются числовыми множествами. Ты уже знаешь множество натуральных чисел, множество целых чисел.
Произвольные множества обозначают большими латинскими буквами А, В, С, ….
Множества могут пересекаться, объединяться.
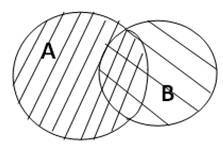
Пусть А – множество всех прямоугольных равнобедренных треугольников, а В – множество всех прямоугольных неравнобедренных треугольников. Если «объединить» эти два множества в одно,  то получим множество всех прямоугольных треугольников.

 Графически объединение множеств А и В удобно изображать, используя диаграмму Эйлера:

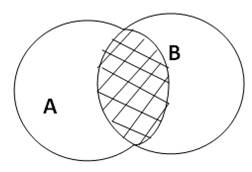
В классе имеется танцевальная группа А и хоровая группа В. учащиеся, являющиеся членами обеих групп, образуют множество, называемое  пересечением множеств А и В.
Графически  удобно пересечение  двух  или более множеств изображать в виде общей части  двух или более кругов Эйлера:

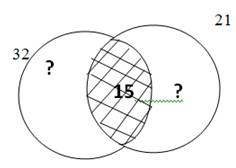
С помощью кругов  Эйлера  можно решать логические задачи на пересечение множеств. 
Например,    задачу  «Из 40 учащихся  шестого класса 32  занимаются в математическом кружке, 21 – в спортивной секции, 15 – и в кружке, и в спортивной секции. Сколько учащихся занимаются только в математическом кружке, и  только в спортивной секции?» можно с помощью кругов Эйлера  изобразить так: