Знакомая незнакомка... или всё о теореме Пифагора: различия между версиями
Материал из Тамбов-Вики
| (не показано 13 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | [[|400 px|right]] | + | [[Файл:Pythagorean_proof2.png|400 px|right]] |
== Название квеста == | == Название квеста == | ||
| − | Знакомая незнакомка | + | Знакомая незнакомка... или всё о теореме Пифагора |
| + | |||
== Авторы идеи == | == Авторы идеи == | ||
*Акулинина Марина Владимировна - преподаватель- организатор ОБЖ Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1» | *Акулинина Марина Владимировна - преподаватель- организатор ОБЖ Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1» | ||
| Строка 51: | Строка 52: | ||
=== Предметные результаты: === | === Предметные результаты: === | ||
| − | + | ''Учащиеся научатся'': | |
| − | работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику | + | * работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику |
| − | |||
* самостоятельно приобретать и применять знания в различных ситуациях для решения несложных практических задач, в том числе с использованием при необходимости справочных материалов | * самостоятельно приобретать и применять знания в различных ситуациях для решения несложных практических задач, в том числе с использованием при необходимости справочных материалов | ||
* выполнять арифметические преобразования выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах | * выполнять арифметические преобразования выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах | ||
* применять изученные понятия, результаты и методы при решении задач различных разделов курса | * применять изученные понятия, результаты и методы при решении задач различных разделов курса | ||
| + | |||
== Возраст участников, межпредметные связи == | == Возраст участников, межпредметные связи == | ||
| − | 8-9 класс | + | 8-9 класс; |
| − | + | ||
| + | ''межпредметные связи:''информатика, история | ||
| + | |||
== Образовательное пространство и ресурсы == | == Образовательное пространство и ресурсы == | ||
| − | + | ||
| − | Участники квеста должны: | + | [https://pifagorkwest.jimdofree.com Виртуальная площадка квеста] |
| − | + | Участники квеста должны иметь: | |
| − | свободный доступ к сети Интернет, | + | * гаджеты с возможностью выполнить качественную видеосъемку, |
| − | + | * свободный доступ к сети Интернет, | |
| − | + | * аккаунт Google, | |
| − | инструкции по работе в сервисах Веб 2.0 | + | * программное обеспечение, позволяющее сканировать QR-код, |
| + | * навыки работы на ПК, | ||
| + | * инструкции по работе в сервисах Веб 2.0 | ||
== Введение: сюжет, роли == | == Введение: сюжет, роли == | ||
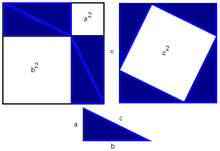
| − | Теорема Пифагора - одна из самых известных геометрических теорем древности. Её помнит каждый человек, который когда-либо учился в средней школе. Даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на | + | Теорема Пифагора - одна из самых известных геометрических теорем древности. Её помнит каждый человек, который когда-либо учился в средней школе. Даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузы, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. |
Теорема Пифагора (без доказательства) встречается еще в вавилонских текстах, написанных за 1200 лет до Пифагора. Она была известна в Древнем Китае и Индии. О прямоугольном треугольнике со сторонами 3;4;5 единиц длины за 200 лет до н.э. знали и египтяне, считая его магическим. | Теорема Пифагора (без доказательства) встречается еще в вавилонских текстах, написанных за 1200 лет до Пифагора. Она была известна в Древнем Китае и Индии. О прямоугольном треугольнике со сторонами 3;4;5 единиц длины за 200 лет до н.э. знали и египтяне, считая его магическим. | ||
| − | + | * Почему знаменитая теорема носит имя Пифагора, хотя была известна задолго до него? | |
| − | + | * Почему теорему Пифагора называют одним из сокровищ геометрии? | |
| − | + | * Как точно разметить прямой угол на местности, не имея специальных инструментов? | |
| − | + | * Сколько существует доказательств теоремы Пифагора и каково её практическое значение? | |
Вы ответите на эти вопросы после прохождения квеста. Вы узнаете много интересного для себя, научитесь применять полученные знания в жизни. | Вы ответите на эти вопросы после прохождения квеста. Вы узнаете много интересного для себя, научитесь применять полученные знания в жизни. | ||
| Строка 88: | Строка 93: | ||
Изучите биографию Пифагора, найдите малоизвестные стороны жизненного и творческого пути великого ученого. Ответьте на вопросы: Почему теорема носит имя Пифагора, если она была известна задолго до его рождения? Какие еще названия есть у знаменитой теоремы? Как появилось выражение "Пифагоровы штаны во все стороны равны"? Результаты исследования представьте в виде интерактивного плаката в серсиве Smore | Изучите биографию Пифагора, найдите малоизвестные стороны жизненного и творческого пути великого ученого. Ответьте на вопросы: Почему теорема носит имя Пифагора, если она была известна задолго до его рождения? Какие еще названия есть у знаменитой теоремы? Как появилось выражение "Пифагоровы штаны во все стороны равны"? Результаты исследования представьте в виде интерактивного плаката в серсиве Smore | ||
| − | *Необходимые инструменты | + | *''Необходимые инструменты'': гаджеты с выходом в Интернет, для работы в серсиве Smore.com |
| − | гаджеты с выходом в Интернет, для работы в серсиве Smore.com | + | *''Форма представления результата'': интерактивный плакат в серсиве Smore.com |
| − | * Форма представления результата | ||
| − | |||
=== Этап 2 === | === Этап 2 === | ||
| Строка 101: | Строка 104: | ||
Изучите различные способы разметки прямого угла на местности. Снимите видеоролик о том, как построить прямой угол, не имея специальных инструментов (транспортира, угольника). Видео разместите на youtube.com | Изучите различные способы разметки прямого угла на местности. Снимите видеоролик о том, как построить прямой угол, не имея специальных инструментов (транспортира, угольника). Видео разместите на youtube.com | ||
| − | *Необходимые инструменты | + | *''Необходимые инструменты:'' гаджеты с камерой, выходом в Интернет для размещения youtube.com |
| − | + | *''Форма представления результата:'' видеоролик | |
| − | * Форма представления результата | ||
| − | |||
=== Этап 3 === | === Этап 3 === | ||
| Строка 112: | Строка 113: | ||
Докажите теорему Пифагора, оформите доказательство с помощью сервиса Google-рисунок | Докажите теорему Пифагора, оформите доказательство с помощью сервиса Google-рисунок | ||
| − | *Необходимые инструменты | + | *''Необходимые инструменты:'' гаджеты с камерой, с выходом в интернет, с приложением, читающим QR-код |
| − | + | *''Форма представления результата:'' Google-рисунок | |
| − | * Форма представления результата | ||
| − | |||
=== Этап 4 === | === Этап 4 === | ||
| Строка 125: | Строка 124: | ||
Придумайте и решите несколько задач практического содержания, в решении которых используется теорема Пифагора. Представьте решения в виде Google - презентации. | Придумайте и решите несколько задач практического содержания, в решении которых используется теорема Пифагора. Представьте решения в виде Google - презентации. | ||
| − | *Необходимые инструменты | + | *''Необходимые инструменты:'' гаджеты с выходом в Интернет, для создания Google - презентации |
| − | + | *''Форма представления результата'': представление решения в виде Google - презентации | |
| − | * Форма представления результата | + | |
| − | |||
| − | |||
| − | |||
== Формирующее и итоговое оценивание == | == Формирующее и итоговое оценивание == | ||
| − | Форма самооценивания и взаимооценивания | + | * Форма самооценивания и взаимооценивания |
| − | Критерии оценивания интерактивного плаката | + | * Критерии оценивания интерактивного плаката |
| − | Критерии оценивания видеоролика | + | * Критерии оценивания видеоролика |
| − | Критерии оценивания Google-рисунок | + | * Критерии оценивания Google-рисунок |
| − | Критерии оценивания Google - презентации | + | * [https://docs.google.com/document/d/1HC_Jt0oqtgwdb8Kat3QDK_f_7AuzZIrjj0R_ymD6VT0/edit?usp=sharing Критерии оценивания Google - презентации] |
| + | |||
== Дополнительные материалы == | == Дополнительные материалы == | ||
[[Категория:Образовательное событие в достижении планируемых метапредметных результатов (Никифоровка)]] | [[Категория:Образовательное событие в достижении планируемых метапредметных результатов (Никифоровка)]] | ||
Текущая версия на 14:21, 16 декабря 2018
Название квеста
Знакомая незнакомка... или всё о теореме Пифагора
Авторы идеи
- Акулинина Марина Владимировна - преподаватель- организатор ОБЖ Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1»
- Бочарова Елена Викторовна - учитель математики Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1»
- Федорова Ольга Анатольевна-учитель начальных классов Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1»
- Баженова Ангелина Александровна - учитель русского языка и литературы Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1»
Тема квеста
История математики, геометрия, реальная математика
Проблемное поле
- Почему знаменитая теорема носит имя Пифагора, хотя была известна задолго до него?
- Почему теорему Пифагора называют одним из сокровищ геометрии?
- Как точно разметить прямой угол на местности, не имея специальных инструментов?
- Сколько существует доказательств теоремы Пифагора и ее практическое значение?
Цель квеста
Использование информационного пространства сети Интернет для знакомства с историей теоремы Пифагора, различными доказательствами теоремы и применением теоремы Пифагора в практической деятельности человека.
Планируемые результаты
Личностные результаты:
- учащихся будут сформированы готовность и способность к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
- умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию
- умение контролировать процесс и результат учебной математической деятельности
Метапредметные результаты:
Регулятивные: учащиеся научатся:
- формулировать и удерживать учебную задачу;
- выбирать действия в соответствии с поставленной задачей и условиями реализации;
- планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
- составлять план и последовательность действий;
- осуществлять контроль по образцу и вносить необходимые коррективы
Познавательные учащиеся научатся:
- самостоятельно выделять и формулировать познавательную цель;
- использовать общие приёмы решения задач;
- применять правила и пользоваться инструкциями и освоенными закономерностями;
- находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме;
- принимать решия, в условиях неполной и избыточной, точной и вероятностной информации
Коммуникативные учащиеся научатся:
- организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников;
- координировать и принимать различные позиции во взаимодействии
Предметные результаты:
Учащиеся научатся:
- работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику
- самостоятельно приобретать и применять знания в различных ситуациях для решения несложных практических задач, в том числе с использованием при необходимости справочных материалов
- выполнять арифметические преобразования выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах
- применять изученные понятия, результаты и методы при решении задач различных разделов курса
Возраст участников, межпредметные связи
8-9 класс;
межпредметные связи:информатика, история
Образовательное пространство и ресурсы
Виртуальная площадка квеста
Участники квеста должны иметь:
- гаджеты с возможностью выполнить качественную видеосъемку,
- свободный доступ к сети Интернет,
- аккаунт Google,
- программное обеспечение, позволяющее сканировать QR-код,
- навыки работы на ПК,
- инструкции по работе в сервисах Веб 2.0
Введение: сюжет, роли
Теорема Пифагора - одна из самых известных геометрических теорем древности. Её помнит каждый человек, который когда-либо учился в средней школе. Даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузы, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. Теорема Пифагора (без доказательства) встречается еще в вавилонских текстах, написанных за 1200 лет до Пифагора. Она была известна в Древнем Китае и Индии. О прямоугольном треугольнике со сторонами 3;4;5 единиц длины за 200 лет до н.э. знали и египтяне, считая его магическим.
- Почему знаменитая теорема носит имя Пифагора, хотя была известна задолго до него?
- Почему теорему Пифагора называют одним из сокровищ геометрии?
- Как точно разметить прямой угол на местности, не имея специальных инструментов?
- Сколько существует доказательств теоремы Пифагора и каково её практическое значение?
Вы ответите на эти вопросы после прохождения квеста. Вы узнаете много интересного для себя, научитесь применять полученные знания в жизни.
Сценарный план квеста
Этап 1
- Ключ
https://learningapps.org/watch?v=pt1d6wfut18
- Задание
Изучите биографию Пифагора, найдите малоизвестные стороны жизненного и творческого пути великого ученого. Ответьте на вопросы: Почему теорема носит имя Пифагора, если она была известна задолго до его рождения? Какие еще названия есть у знаменитой теоремы? Как появилось выражение "Пифагоровы штаны во все стороны равны"? Результаты исследования представьте в виде интерактивного плаката в серсиве Smore
- Необходимые инструменты: гаджеты с выходом в Интернет, для работы в серсиве Smore.com
- Форма представления результата: интерактивный плакат в серсиве Smore.com
Этап 2
- Ключ
https://learningapps.org/watch?v=pay98y0xa18
- Задание
Изучите различные способы разметки прямого угла на местности. Снимите видеоролик о том, как построить прямой угол, не имея специальных инструментов (транспортира, угольника). Видео разместите на youtube.com
- Необходимые инструменты: гаджеты с камерой, выходом в Интернет для размещения youtube.com
- Форма представления результата: видеоролик
Этап 3
- Задание
Докажите теорему Пифагора, оформите доказательство с помощью сервиса Google-рисунок
- Необходимые инструменты: гаджеты с камерой, с выходом в интернет, с приложением, читающим QR-код
- Форма представления результата: Google-рисунок
Этап 4
- Ключ
https://learningapps.org/watch?v=pxizw77u218
- Задание
Придумайте и решите несколько задач практического содержания, в решении которых используется теорема Пифагора. Представьте решения в виде Google - презентации.
- Необходимые инструменты: гаджеты с выходом в Интернет, для создания Google - презентации
- Форма представления результата: представление решения в виде Google - презентации
Формирующее и итоговое оценивание
- Форма самооценивания и взаимооценивания
- Критерии оценивания интерактивного плаката
- Критерии оценивания видеоролика
- Критерии оценивания Google-рисунок
- Критерии оценивания Google - презентации