Знакомая незнакомка... или всё о теореме Пифагора: различия между версиями
Материал из Тамбов-Вики
| (не показано 18 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | [[|400 px|right]] | + | [[Файл:Pythagorean_proof2.png|400 px|right]] |
== Название квеста == | == Название квеста == | ||
| − | Знакомая незнакомка | + | Знакомая незнакомка... или всё о теореме Пифагора |
| + | |||
== Авторы идеи == | == Авторы идеи == | ||
*Акулинина Марина Владимировна - преподаватель- организатор ОБЖ Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1» | *Акулинина Марина Владимировна - преподаватель- организатор ОБЖ Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1» | ||
| Строка 12: | Строка 13: | ||
История математики, геометрия, реальная математика | История математики, геометрия, реальная математика | ||
== Проблемное поле == | == Проблемное поле == | ||
| − | Почему знаменитая теорема носит имя Пифагора, хотя была известна задолго до него? Почему теорему Пифагора называют одним из сокровищ геометрии? Как точно разметить прямой угол на местности, не имея специальных инструментов? Сколько существует доказательств теоремы Пифагора ее практическое значение? | + | * Почему знаменитая теорема носит имя Пифагора, хотя была известна задолго до него? |
| + | * Почему теорему Пифагора называют одним из сокровищ геометрии? | ||
| + | * Как точно разметить прямой угол на местности, не имея специальных инструментов? | ||
| + | * Сколько существует доказательств теоремы Пифагора и ее практическое значение? | ||
| + | |||
== Цель квеста == | == Цель квеста == | ||
| − | + | Использование информационного пространства сети Интернет для знакомства с историей теоремы Пифагора, различными доказательствами теоремы и применением теоремы Пифагора в практической деятельности человека. | |
== Планируемые результаты == | == Планируемые результаты == | ||
| Строка 26: | Строка 31: | ||
=== Метапредметные результаты: === | === Метапредметные результаты: === | ||
| − | + | '''Регулятивные''': | |
| − | учащиеся научатся: | + | ''учащиеся научатся:'' |
| − | + | * формулировать и удерживать учебную задачу; | |
| − | + | * выбирать действия в соответствии с поставленной задачей и условиями реализации; | |
| − | + | * планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; | |
| − | учащиеся научатся: | + | * составлять план и последовательность действий; |
| − | самостоятельно выделять и формулировать познавательную цель; использовать общие приёмы решения задач; применять правила и пользоваться инструкциями и освоенными закономерностями; находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать | + | * осуществлять контроль по образцу и вносить необходимые коррективы |
| − | + | '''Познавательные''' | |
| − | + | ''учащиеся научатся:'' | |
| − | учащиеся научатся: | + | * самостоятельно выделять и формулировать познавательную цель; |
| − | организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников; координировать и принимать различные позиции во взаимодействии | + | * использовать общие приёмы решения задач; |
| − | + | * применять правила и пользоваться инструкциями и освоенными закономерностями; | |
| + | * находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; | ||
| + | * принимать решия, в условиях неполной и избыточной, точной и вероятностной информации | ||
| + | '''Коммуникативные''' | ||
| + | ''учащиеся научатся:'' | ||
| + | *организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников; | ||
| + | * координировать и принимать различные позиции во взаимодействии | ||
=== Предметные результаты: === | === Предметные результаты: === | ||
| − | + | ''Учащиеся научатся'': | |
| − | работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику | + | * работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику |
| − | |||
* самостоятельно приобретать и применять знания в различных ситуациях для решения несложных практических задач, в том числе с использованием при необходимости справочных материалов | * самостоятельно приобретать и применять знания в различных ситуациях для решения несложных практических задач, в том числе с использованием при необходимости справочных материалов | ||
* выполнять арифметические преобразования выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах | * выполнять арифметические преобразования выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах | ||
* применять изученные понятия, результаты и методы при решении задач различных разделов курса | * применять изученные понятия, результаты и методы при решении задач различных разделов курса | ||
| + | |||
== Возраст участников, межпредметные связи == | == Возраст участников, межпредметные связи == | ||
| − | 8-9 класс | + | 8-9 класс; |
| − | + | ||
| + | ''межпредметные связи:''информатика, история | ||
| + | |||
== Образовательное пространство и ресурсы == | == Образовательное пространство и ресурсы == | ||
| − | + | ||
| − | Участники квеста должны: | + | [https://pifagorkwest.jimdofree.com Виртуальная площадка квеста] |
| − | + | Участники квеста должны иметь: | |
| − | свободный доступ к сети Интернет, | + | * гаджеты с возможностью выполнить качественную видеосъемку, |
| − | + | * свободный доступ к сети Интернет, | |
| − | + | * аккаунт Google, | |
| − | инструкции по работе в сервисах Веб 2.0 | + | * программное обеспечение, позволяющее сканировать QR-код, |
| + | * навыки работы на ПК, | ||
| + | * инструкции по работе в сервисах Веб 2.0 | ||
== Введение: сюжет, роли == | == Введение: сюжет, роли == | ||
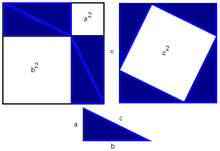
| − | Теорема Пифагора - одна из самых известных геометрических теорем древности. Её помнит каждый человек, который когда-либо учился в средней школе. Даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на | + | Теорема Пифагора - одна из самых известных геометрических теорем древности. Её помнит каждый человек, который когда-либо учился в средней школе. Даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузы, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. |
Теорема Пифагора (без доказательства) встречается еще в вавилонских текстах, написанных за 1200 лет до Пифагора. Она была известна в Древнем Китае и Индии. О прямоугольном треугольнике со сторонами 3;4;5 единиц длины за 200 лет до н.э. знали и египтяне, считая его магическим. | Теорема Пифагора (без доказательства) встречается еще в вавилонских текстах, написанных за 1200 лет до Пифагора. Она была известна в Древнем Китае и Индии. О прямоугольном треугольнике со сторонами 3;4;5 единиц длины за 200 лет до н.э. знали и египтяне, считая его магическим. | ||
| − | + | * Почему знаменитая теорема носит имя Пифагора, хотя была известна задолго до него? | |
| − | + | * Почему теорему Пифагора называют одним из сокровищ геометрии? | |
| − | + | * Как точно разметить прямой угол на местности, не имея специальных инструментов? | |
| − | + | * Сколько существует доказательств теоремы Пифагора и каково её практическое значение? | |
Вы ответите на эти вопросы после прохождения квеста. Вы узнаете много интересного для себя, научитесь применять полученные знания в жизни. | Вы ответите на эти вопросы после прохождения квеста. Вы узнаете много интересного для себя, научитесь применять полученные знания в жизни. | ||
| Строка 78: | Строка 93: | ||
Изучите биографию Пифагора, найдите малоизвестные стороны жизненного и творческого пути великого ученого. Ответьте на вопросы: Почему теорема носит имя Пифагора, если она была известна задолго до его рождения? Какие еще названия есть у знаменитой теоремы? Как появилось выражение "Пифагоровы штаны во все стороны равны"? Результаты исследования представьте в виде интерактивного плаката в серсиве Smore | Изучите биографию Пифагора, найдите малоизвестные стороны жизненного и творческого пути великого ученого. Ответьте на вопросы: Почему теорема носит имя Пифагора, если она была известна задолго до его рождения? Какие еще названия есть у знаменитой теоремы? Как появилось выражение "Пифагоровы штаны во все стороны равны"? Результаты исследования представьте в виде интерактивного плаката в серсиве Smore | ||
| − | *Необходимые инструменты | + | *''Необходимые инструменты'': гаджеты с выходом в Интернет, для работы в серсиве Smore.com |
| − | гаджеты с выходом в Интернет, для работы в серсиве Smore.com | + | *''Форма представления результата'': интерактивный плакат в серсиве Smore.com |
| − | * Форма представления результата | ||
| − | |||
=== Этап 2 === | === Этап 2 === | ||
| Строка 91: | Строка 104: | ||
Изучите различные способы разметки прямого угла на местности. Снимите видеоролик о том, как построить прямой угол, не имея специальных инструментов (транспортира, угольника). Видео разместите на youtube.com | Изучите различные способы разметки прямого угла на местности. Снимите видеоролик о том, как построить прямой угол, не имея специальных инструментов (транспортира, угольника). Видео разместите на youtube.com | ||
| − | *Необходимые инструменты | + | *''Необходимые инструменты:'' гаджеты с камерой, выходом в Интернет для размещения youtube.com |
| − | + | *''Форма представления результата:'' видеоролик | |
| − | * Форма представления результата | ||
| − | |||
=== Этап 3 === | === Этап 3 === | ||
| Строка 102: | Строка 113: | ||
Докажите теорему Пифагора, оформите доказательство с помощью сервиса Google-рисунок | Докажите теорему Пифагора, оформите доказательство с помощью сервиса Google-рисунок | ||
| − | *Необходимые инструменты | + | *''Необходимые инструменты:'' гаджеты с камерой, с выходом в интернет, с приложением, читающим QR-код |
| − | + | *''Форма представления результата:'' Google-рисунок | |
| − | * Форма представления результата | ||
| − | |||
=== Этап 4 === | === Этап 4 === | ||
| Строка 115: | Строка 124: | ||
Придумайте и решите несколько задач практического содержания, в решении которых используется теорема Пифагора. Представьте решения в виде Google - презентации. | Придумайте и решите несколько задач практического содержания, в решении которых используется теорема Пифагора. Представьте решения в виде Google - презентации. | ||
| − | *Необходимые инструменты | + | *''Необходимые инструменты:'' гаджеты с выходом в Интернет, для создания Google - презентации |
| − | + | *''Форма представления результата'': представление решения в виде Google - презентации | |
| − | * Форма представления результата | + | |
| − | |||
| − | |||
| − | |||
== Формирующее и итоговое оценивание == | == Формирующее и итоговое оценивание == | ||
| − | Форма самооценивания и взаимооценивания | + | * Форма самооценивания и взаимооценивания |
| − | Критерии оценивания интерактивного плаката | + | * Критерии оценивания интерактивного плаката |
| − | Критерии оценивания видеоролика | + | * Критерии оценивания видеоролика |
| − | Критерии оценивания Google-рисунок | + | * Критерии оценивания Google-рисунок |
| − | Критерии оценивания Google - презентации | + | * [https://docs.google.com/document/d/1HC_Jt0oqtgwdb8Kat3QDK_f_7AuzZIrjj0R_ymD6VT0/edit?usp=sharing Критерии оценивания Google - презентации] |
| + | |||
== Дополнительные материалы == | == Дополнительные материалы == | ||
[[Категория:Образовательное событие в достижении планируемых метапредметных результатов (Никифоровка)]] | [[Категория:Образовательное событие в достижении планируемых метапредметных результатов (Никифоровка)]] | ||
Текущая версия на 14:21, 16 декабря 2018
Название квеста
Знакомая незнакомка... или всё о теореме Пифагора
Авторы идеи
- Акулинина Марина Владимировна - преподаватель- организатор ОБЖ Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1»
- Бочарова Елена Викторовна - учитель математики Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1»
- Федорова Ольга Анатольевна-учитель начальных классов Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1»
- Баженова Ангелина Александровна - учитель русского языка и литературы Сабуро - Покровского филиала МБОУ «Никифоровская СОШ №1»
Тема квеста
История математики, геометрия, реальная математика
Проблемное поле
- Почему знаменитая теорема носит имя Пифагора, хотя была известна задолго до него?
- Почему теорему Пифагора называют одним из сокровищ геометрии?
- Как точно разметить прямой угол на местности, не имея специальных инструментов?
- Сколько существует доказательств теоремы Пифагора и ее практическое значение?
Цель квеста
Использование информационного пространства сети Интернет для знакомства с историей теоремы Пифагора, различными доказательствами теоремы и применением теоремы Пифагора в практической деятельности человека.
Планируемые результаты
Личностные результаты:
- учащихся будут сформированы готовность и способность к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
- умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию
- умение контролировать процесс и результат учебной математической деятельности
Метапредметные результаты:
Регулятивные: учащиеся научатся:
- формулировать и удерживать учебную задачу;
- выбирать действия в соответствии с поставленной задачей и условиями реализации;
- планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
- составлять план и последовательность действий;
- осуществлять контроль по образцу и вносить необходимые коррективы
Познавательные учащиеся научатся:
- самостоятельно выделять и формулировать познавательную цель;
- использовать общие приёмы решения задач;
- применять правила и пользоваться инструкциями и освоенными закономерностями;
- находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме;
- принимать решия, в условиях неполной и избыточной, точной и вероятностной информации
Коммуникативные учащиеся научатся:
- организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников;
- координировать и принимать различные позиции во взаимодействии
Предметные результаты:
Учащиеся научатся:
- работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику
- самостоятельно приобретать и применять знания в различных ситуациях для решения несложных практических задач, в том числе с использованием при необходимости справочных материалов
- выполнять арифметические преобразования выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах
- применять изученные понятия, результаты и методы при решении задач различных разделов курса
Возраст участников, межпредметные связи
8-9 класс;
межпредметные связи:информатика, история
Образовательное пространство и ресурсы
Виртуальная площадка квеста
Участники квеста должны иметь:
- гаджеты с возможностью выполнить качественную видеосъемку,
- свободный доступ к сети Интернет,
- аккаунт Google,
- программное обеспечение, позволяющее сканировать QR-код,
- навыки работы на ПК,
- инструкции по работе в сервисах Веб 2.0
Введение: сюжет, роли
Теорема Пифагора - одна из самых известных геометрических теорем древности. Её помнит каждый человек, который когда-либо учился в средней школе. Даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузы, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. Теорема Пифагора (без доказательства) встречается еще в вавилонских текстах, написанных за 1200 лет до Пифагора. Она была известна в Древнем Китае и Индии. О прямоугольном треугольнике со сторонами 3;4;5 единиц длины за 200 лет до н.э. знали и египтяне, считая его магическим.
- Почему знаменитая теорема носит имя Пифагора, хотя была известна задолго до него?
- Почему теорему Пифагора называют одним из сокровищ геометрии?
- Как точно разметить прямой угол на местности, не имея специальных инструментов?
- Сколько существует доказательств теоремы Пифагора и каково её практическое значение?
Вы ответите на эти вопросы после прохождения квеста. Вы узнаете много интересного для себя, научитесь применять полученные знания в жизни.
Сценарный план квеста
Этап 1
- Ключ
https://learningapps.org/watch?v=pt1d6wfut18
- Задание
Изучите биографию Пифагора, найдите малоизвестные стороны жизненного и творческого пути великого ученого. Ответьте на вопросы: Почему теорема носит имя Пифагора, если она была известна задолго до его рождения? Какие еще названия есть у знаменитой теоремы? Как появилось выражение "Пифагоровы штаны во все стороны равны"? Результаты исследования представьте в виде интерактивного плаката в серсиве Smore
- Необходимые инструменты: гаджеты с выходом в Интернет, для работы в серсиве Smore.com
- Форма представления результата: интерактивный плакат в серсиве Smore.com
Этап 2
- Ключ
https://learningapps.org/watch?v=pay98y0xa18
- Задание
Изучите различные способы разметки прямого угла на местности. Снимите видеоролик о том, как построить прямой угол, не имея специальных инструментов (транспортира, угольника). Видео разместите на youtube.com
- Необходимые инструменты: гаджеты с камерой, выходом в Интернет для размещения youtube.com
- Форма представления результата: видеоролик
Этап 3
- Задание
Докажите теорему Пифагора, оформите доказательство с помощью сервиса Google-рисунок
- Необходимые инструменты: гаджеты с камерой, с выходом в интернет, с приложением, читающим QR-код
- Форма представления результата: Google-рисунок
Этап 4
- Ключ
https://learningapps.org/watch?v=pxizw77u218
- Задание
Придумайте и решите несколько задач практического содержания, в решении которых используется теорема Пифагора. Представьте решения в виде Google - презентации.
- Необходимые инструменты: гаджеты с выходом в Интернет, для создания Google - презентации
- Форма представления результата: представление решения в виде Google - презентации
Формирующее и итоговое оценивание
- Форма самооценивания и взаимооценивания
- Критерии оценивания интерактивного плаката
- Критерии оценивания видеоролика
- Критерии оценивания Google-рисунок
- Критерии оценивания Google - презентации